I. Tập hợp số thực
1. Số thực
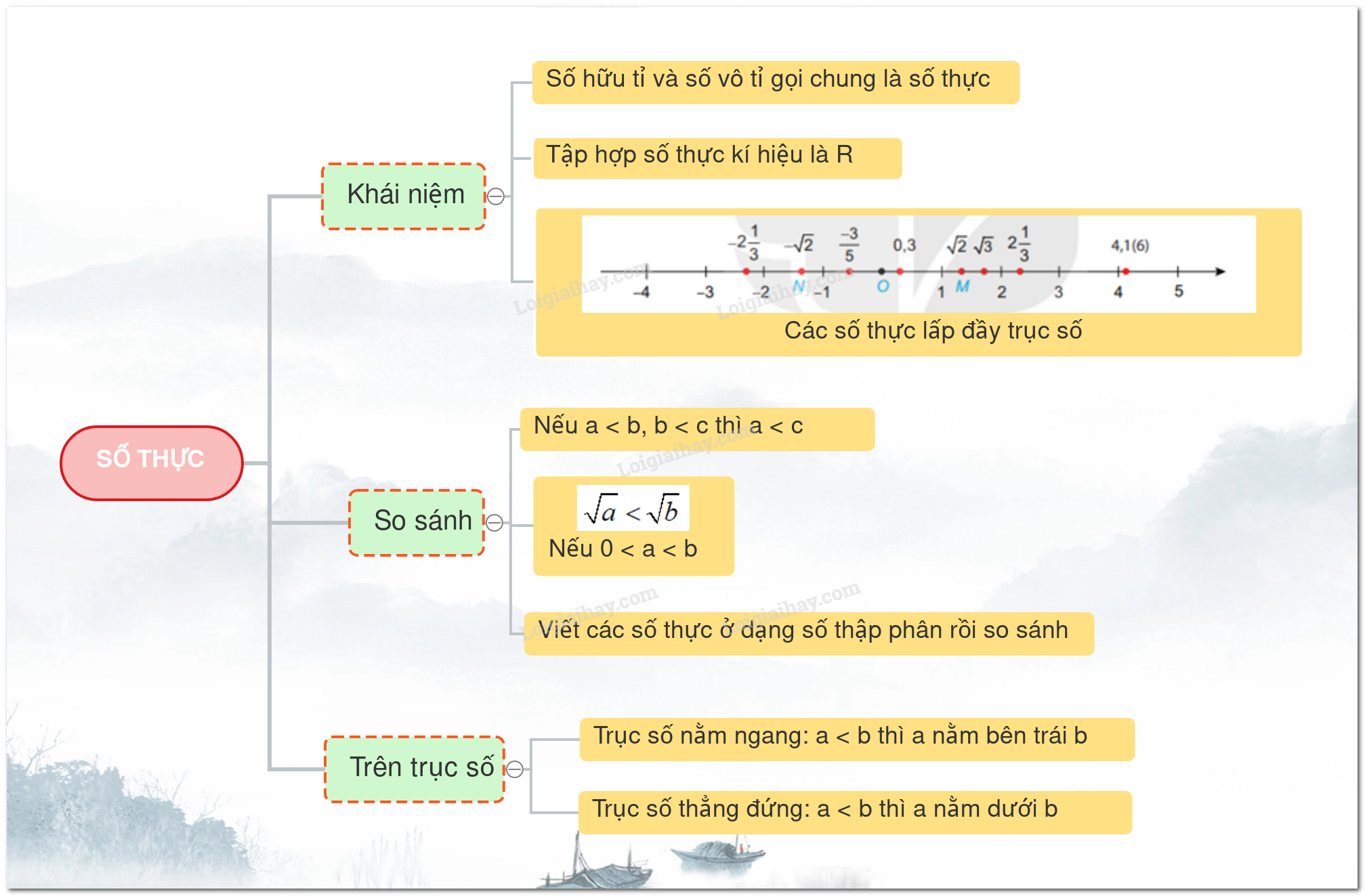
* Số hữu tỉ và số vô tỉ gọi chung là số thực
* Tập hợp các số thực được kí hiệu là R.
2. Biểu diễn thập phân của số thực
II. Biểu diễn số thực trên trục số
+ Trong tập số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.
* Trục số thực được biểu diễn bởi 1 số điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.
Chú ý: Các số thực lấp đầy trục số.
III. Số đối của một số thực
+ Mỗi số thực a đều có một số đối là -a
+ Trên trục số, 2 điểm biểu diễn 2 số thực đối nhau a và -a nằm về 2 phía khác nhau so với điểm O và có cùng khoảng cách đến O.
+ Số đối của số 0 là 0
Ví dụ: -\(\sqrt 5 \) là số đối của \(\sqrt 5 \)
IV. So sánh hai số thực
1. So sánh 2 số thực
+ Với 2 số thực a và b bất kì, ta luôn có hoặc a = b, hoặc a < b, hoặc a > b
+ Cho 3 số thực a, b, c. Nếu a < b; b < c thì a < c ( Tính chất bắc cầu)
+ Các số thực lớn hơn 0 gọi là các số thực dương.
+ Các số thực nhỏ hơn 0 gọi là các số thực âm.
+ Số 0 không là số thực âm, cũng không là số thực dương.
2. Cách so sánh hai số thực:
Ta viết chúng về cùng dạng phân số (hoặc dạng số thập phân) rồi so sánh chúng.
* Các số thực đều viết được dưới dạng số thập phân ( hữu hạn hay vô hạn). Ta có thể so sánh 2 số thực tương tự như so sánh số thập phân.
Ví dụ:
0,322 … < 0,324… nên 0,3(2) < 0,324…
Chú ý: Nếu 0 < a < b thì \(\sqrt a < \sqrt b \)
Ví dụ: Vì 3 < 4 nên \(\sqrt 3 < \sqrt 4 = 2\)
3. Minh họa trên trục số
* Trên trục số nằm ngang:
+ Nếu a < b thì điểm a nằm bên trái điểm b
+ Nếu điểm a nằm bên trái điểm b thì a < b
+ Các điểm nằm bên trái gốc O biểu diễn số hữu tỉ âm; các điểm nằm bên phải gốc O biểu diễn số hữu tỉ dương.
* Trên trục số thẳng đứng:
+ Nếu a < b thì điểm a nằm phía dưới điểm b
+ Nếu điểm a nằm phía dưới điểm b thì a < b
+ Các điểm nằm phía dưới gốc O biểu diễn số hữu tỉ âm; các điểm nằm phía trên gốc O biểu diễn số hữu tỉ dương.








 Bùi Việt
Bùi Việt